Вероятностный характер прогнозирования

1. Что такое вероятностный характер прогнозирования

Вероятностный характер прогнозирования, это когда среди каких-нибудь прогнозов развития ситуации нет ни одного прогноза с вероятностью его исполнения равной 1.

1.1. Пример прогнозирования без вероятностного характера

Допустим, вы держите в руке камень и отпускаете его. Надо сделать прогноз, что станет с камнем. У вас есть 5 вариантов разных прогнозов:

1. Камень упадет вниз на землю и будет лежать на земле.
2. Камень останется висеть неподвижно в воздухе.
3. Камень полетит вверх и улетит в космос.
4. Камень полетит вбок и улетит очень далеко.
5. Камень начала упадет на землю, а потом отскочит от земли и улетит в космос.

В этом примере первый прогноз сбывается с вероятностью равной 1, а все остальные прогнозы сбываются с нулевой вероятностью. То есть нет промежуточных вероятностей больше нуля и меньше единицы. Значит, в этой ситуации прогнозирование не имеет вероятностного характера.

Если всё время в такой ситуации давать прогноз номер 1, то этот прогноз всегда будет сбываться. Ошибок прогнозирования не будет.

1.2. Пример прогнозирования с вероятностным характером

Допустим, вы подкидываете монету. У вас есть 4 варианта разных прогнозов:

1. Монета упадет решкой вверх.
2. Монета упадет орлом вверх.
3. Монету упадет на ребро и останется в таком положении.
4. Монета при подбрасывании улетит в космос и мы никогда не узнаем результат.

Вероятность исполнения первого прогноза равна 1/2. Вероятность исполнения второго прогноза тоже 1/2. А у 3-го и 4-го прогнозов вероятности исполнения нулевые. Здесь нет ни одного прогноза с вероятностью исполнения равной 1.

Может мы забыли добавить к этому списку еще какой-нибудь 5-й пункт прогноза, который как раз и исполнится с вероятностью единица?

Нет, не забыли. Любые другие пункты, которые можно придумать, будут иметь только нулевую вероятность, а не единицу. Дело в том, что сумма всех вероятностей должна быть равно 1. А у нас эта сумма уже набрана при сложении вероятностей первого и второго прогнозов (1/2 + 1/2 = 1). То есть всё, что можно добавить к этому списку будет иметь только нулевую вероятность исполнения прогноза.

Итак прогнозирование результата подкидывания монеты носить принципиально вероятностный характер, так как ни один прогноз не исполняется с вероятностью 1. При прогнозировании в 50% всех случаев у вас будет ошибочный прогноз.

1.3. Замечание

Обратите внимание, что при вероятностном характере прогнозирования совсем не обязательно, чтобы прогнозы сбывались с одинаковыми вероятностями. Например, при подкидывании кривой монеты, решка может выпадать с вероятносстью 0.1, а орел с вероятностью 0.9.

Но прогнозирование всё равно будет иметь вероятностный характер. Если вы будете прогнозировать всё время выпадение орла, то вы в 10% будете ошибаться.

2. Вероятностный характер прогнозов рыночных цен

Прогнозы рыночных цен имеют вероятностный характер. Давайте посмотрим, как это понимается и что за этим стоит.

Вероятностный характер прогнозирования биржевых цен обусловлен двумя факторами:

• Частично случайное поведение цен. Поведение цены во времени складывается из двух слагаемых: детерминированного поведения и случайного. Случайная компонента поведение цены обусловлена тем, что поведение участников рынка часто бывает случайным. Например из-за неожиданного крупного случайного события, типа начало войны, терракт, авиакатастрофа, санкции, землетрясение, несчастный случай с наследным принцем и т.п. Или из-за неожиданого мелкого случайного события в личной жизни незначительного участника рынка, типа опоздание на работу, отвлечение на телефонный звонок, неожиданные семейные обстоятельства, проблемы со здоровьем, и т.п.
• Эффект бабочки. Последнее замечание о мелких случайных событий в жизни какого-нибудь незначительного участника рынка на первый взгляд кажутся несерьезными. Обычно, люди представляют себе, что таких событий очень много и они разнонаправлены, и поэтому, будто бы, эти факторы взаимно компенсируются и не оказывают какого-то влияния на биржевые цены. На самом деле всё не так просто. Рынок часто бывает в очень неустойчивом состоянии, таком неустойчивом, что даже маленкая флуктуация способна привести к сильным ценовым сдвигам, подобным сходу лавины. Как правило такие вещи происходят при надувании рыночных пузырей.

Вероятностный характер прогнозов имеет два следствия. Одно из них, в общем-то, тривиальное, а вот второе совсем не такое очевидное, как первое:

1. Ни один метод прогнозирования никогда не может давать всегда правильные прогнозы с заходимостью 100%.
2. Чтобы проявились статистические закономерности какой-нибудь торговой системы, надо совершить достаточно большое количество сделок.

Посмотрим на это более подробно.

Вероятностный характер прогнозирования рыночных цен означает, что никогда не бывает так, чтобы очень продолжительное число раз прогнозы всё время были только всегда верными. Другими словами не существует однозначной детерминированной формулы, по которой можно математически всегда вычислять только правильные прогнозы. То есть не существует такого метода прогнозирования, который в среде трейдеров называется Граалем.

Почему так, а не иначе?

Потому что, если бы существовал такой Грааль, то это означало бы, что прогнозы исполняются с вероятностью p = 1. А любое событие с такой вероятностью является не вероятным, а неизбежным и достоверным. То есть в таком случае у нас отсутствовал бы вероятностный характер прогнозирования. А это противоречит природе рынка.

Точно также никогда не бывает так, чтобы очень продолжительное число раз прогнозы всё время были только всегда ошибочными. Ведь в этом случае прогнозы исполнялись бы с вероятностью p = 0. А любое событие с такой нулевой вероятностью является не вероятным, а всегда невозможным. То есть в таком случае у нас тоже отсутствует вероятностный характер прогнозирования, что противоречит природе рынка.

Таким образом, невозможно сделать так, чтобы все торговые сделки были бы только в плюс. Всегда часть сделок обязательно ДОЛЖНА быть в минус.

Точно также невозможно сделать так, чтобы все торговые сделки были бы только убыточными. Всегда часть сделок будет прибыльной.

Это сильно напоминает тепловую машину в термодинамике. В тепловой машине никогда не бывает так, чтобы всё тепло перешло в полезную работу. Часть тепла обязательно будет рассеяно в окружающем пространстве. Эффективность тепловой машины показывает её Коэффициент Полезного действия (КПД). Её КПД принципиально никогда не может быть равен единице (100%).

Точно также и в трейдинге. Часть финансов трейдера всегда теряется на убыточных сделках. Это и есть аналог диссипации энергии тепловой машины.

3. Распределение выигрышей

Допустим, какой-то сигнальщик утверждает, что его сигналы заходят на 70%. То есть 70% всех его прогнозов направления движения цены будто бы оказываются верными. Допустим, что этот сигнальщик не врет, что так оно и есть.

Вопрос на засыпку: Если вы воспользуетесь его прогнозами 10 раз, то сколько ваших сделок будут прибыльными?

Или еще более конкретнее: У вас будет 7 прибыльных сделок из 10 или их будет не семь?

Ответ: Скорее всего, у вас число прибыльных сделок не будет равно 7. Более вероятно, что число прибыльных сделок будет не равно семи.

Почему это так, а не иначе?

Давайте разберемся.

3.1. Пример игры в орлянку

Допустим, вы играете в орлянку. Если при подбрасывании монеты выпадает решка, то вы проигрываете. А если выпадает орел, то вы выигрываете.

Вероятность выпадения орла p = 1/2. Поэтому, на первый взгляд, кажется, что если подбрасывать монету несколько раз сериями по 10 подбрасываний, то в большинстве случаев из каждых 10 бросков в 5 случаях будет выпадать орел.

Но если вы реально проведете такой эксперимент, то обнаружите, что в большинстве случаев орел выпадает не 5 раз из каждых 10 бросков. В большинстве случаев орел выпадает какое-то другое количество раз отличное от 5 выпадений.

Конечно, 5 выпаданий орла будет встречаться гораздо чаще, чем, например, 4 выпаданий из 10 или чем 6 выпаданий из 10. А тем более чаще, чем орел будет выпадать 3 раза из 10 или 7 раз из 10. Но в сумме выпадений орла не 5 раз будет больше, чем выпадений орла точно 5 раз из 10 бросаний монеты.

А в среднем получится 5 из 10 из-за симметрии. Ведь 4 из 10 выпадает примерно столько же раз, сколько и 6 из 10. А среднее между 4 и 6 равно 5. Также и 3 из 10 выпадает примерно столько же, как и 7 из 10. А среднее между 3 и 7 равно 5. И т.д. Поэтому, в среднем, получается, что орел всё таки выпадает в половине всех бросков монеты, хотя 5 из каждых 10 встречается не так часто.

Почему же это именно так, а не иначе?

Потому что из-за вероятностного характера выпадения орла существует распределение числа выпадения орлов при бросании монеты. То есть вероятность выпадения 5 орлов из 10 бросков не равна в точности единице (p ≠ 1). Если бы эта вероятность в точности равнялась бы единице, то это было бы достоверным событием, а не вероятностным событием. То есть отсутствовал бы вероятностный характер выпадения орла при бросании монеты.

Если пренебречь очень маловероятным событием выпадения монеты на ребро, то вероятность выпадения орла M раз из N бросков определяется следующим частным случаем биномиального распределения:

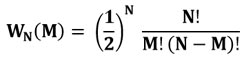
Здесь N, это сколько раз подкинули монету; M, это сколько раз при этом выпал орел; а W_N(M), это вероятность выпадений M орлов при N подбрасываний монеты. Понятно, что M не может быть больше N, то есть всегда 0 ≤ M ≤ N.

Посмотрим, как пользоваться такой формулой.

Посчитаем по этой формуле все W_N(M) для N от 1 до 4. Результат показан в таблице ниже.

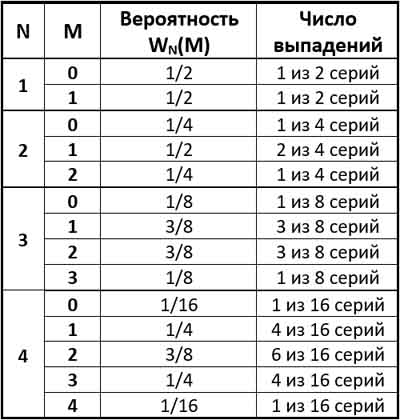
Подробно посмотрим случай, когда монету подкидываем 4 раза (N = 4). Наивно ожидать, что в таком случае орел будет всегда выпадать 2 раза на каждые 4 броска монеты. Для N = 4 будет W₄(2) = 3/8, а не 1. Это значит, что если 8 раз подбрасывать монету сериями по 4 раза, то из 8-и серий примерно только в 3-х сериях орел выпадет 2 раза. В остальных 5 сериях по 4 броска орел выпадет не 2 раза, а другое количество раз.

В последней колонке таблицы показано сколько раз выпадет орел в 4-х бросках, если 16 раз сделаем по 4 броска. Как видите, примерно в одном случае орел, вообще, не выпадет (M = 0). А также в одной серии из 16 серий орел выпадет все 4 раза (M = 4).

3.2. Выигрыши в трейдинге

В трейдинге независимые выигрыши также распределены по биномиальному распределению, которое в общем виде имеет вид:

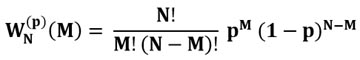
Здесь p, это вероятность того, что сделка окажется прибыльной. В случае с нашим сигнальщиком, который утверждает, что его прогнозы исполняются в 70%, эта вероятность будет p = 0.7.

Все остальные обозначения такие же, как и в предыдущем разделе: N - число проведенных сделок, M - число выигрышей, а W_N^(p)(M), это вероятность того, что из N сделок будет M выигрышей при условии, что вероятность выигрыша равна p.

Посмотрим, какая будет разница, если по сигналам нашего сигнальщика мы проведем 5, 10 и 100 сделок. При этом допустим, что нам надо обеспечить, чтобы более 60% всех наших сделок были прибыльными.

То есть считаем, что только более 60% прибыльных сделок дает нам положительное математическое ожидание. Только в таком случае будет рост стартового капилала. Если прибыльных сделок 60% или меньше, то математическое ожидание меньше нуля, то есть стартовый капитал уменьшится.

Более подробную информацию про математическое ожидание и пограничный процент прибыльных сделок на бинарных опционах можно посмотреть в статье "Главная формула бинарных опционов". На Форексе, фондовой бирже и криптобирже математическое ожидание и пограничный процент достаточного количества прибыльных сделок сложно зависят от расстановки ордеров TakeProfit и StopLoss, а также от величины кредитного плеча и доли капитала на каждую сделку. Для расчета минимальной доли прибыльных сделок можно использовать Калькулятор минимально необходимого количества прибыльных сделок.

3.2.1. Пять сделок

Ниже на графике показаны вероятности определенного количества прибыльных сделок, если всего было проведено N = 5 сделок, а вероятность того, что сделка будет прибыльной p = 0.7. По горизонтальной оси показано, сколько было прибыльных сделок M среди 5-и сделок. По вертикальной оси показано, какова будет вероятность того, что это M будет иметь место в 5-и сделках.

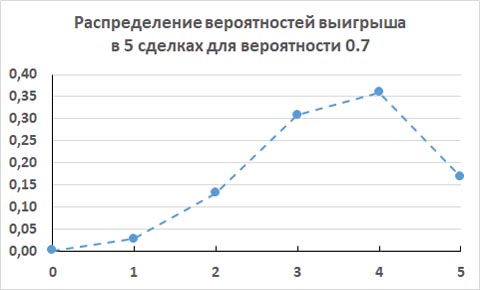
Нам нужно, чтобы прибыльными были или все 5 сделок или 4 сделки из 5-и сделок. Тогда стартовый капитал увеличится. Если из 5-и сделок прибыльными будет только 3 сделки, то стартовый капитал уменьшится, так как 3 от 5-и, это уже 60%, а мы договорились что при 60% суммарно получаются убытки.

Давайте просуммируем все вероятности количества прибыльных сделок из 5 от 0 до 3. Получаем 0.47178. То есть, если трейдер сделает только 5 сделок по сигналам рассматриваемого сигнальщика, то примерно с вероятностью 0.47 он получит убытки.

Или, по другому, если 100 трейдеров попробуют в разное время использовать сигналы рассматриваемого сигнальщика, то примерно 47 трейдеров получит убытки. А в плюсе останется примерно 53 трейдера из этих 100. Это умозрительный эксперимент, поэтому вариант разорения не учитываем. То есть считаем, что все трейдеры соблюдают правила финансового менеджмента и, что у всех 100 трейдеров достаточно большой стартовый капитал, такой, что за 5 сделок разориться невозможно, даже если все 5 сделок будут убыточными.

3.2.2. Десять сделок

Аналогично, ниже показан график для случая, когда проводится 10 сделок. Этот график также построен с помощью общей формулы биноминального распределения.

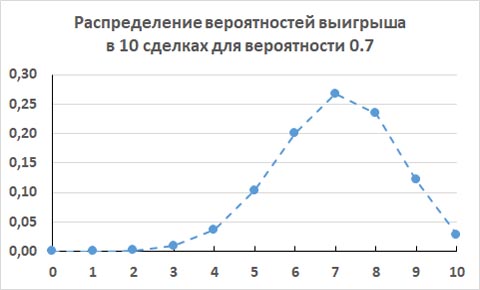
Теперь 60% от 10 сделок, это 6 сделок. Чтобы оказаться в плюсе, надо чтобы из 10 сделок прибыльными оказались 7, или 8, или 9, или все 10 сделок.

Суммируем все вероятности от 0 до 6 прибыльных сделок из 10 и получаем примерно 0.3504. Это уже лучше. Теперь из 100 трейдеров в минусе окажется только примерно 35 трейдеров, а в плюсе будет примено 65 трейдеров.

3.2.3. Сто сделок

Наконец, посмотрим, каковы шансы остаться в плюсе, если проведем 100 сделок.

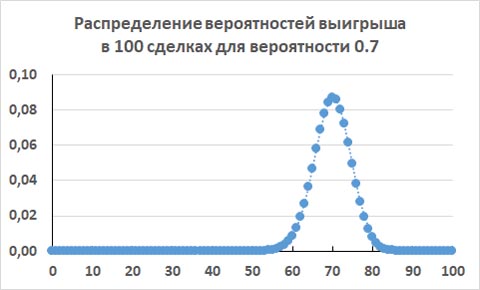
Если просуммировать все значения вероятностей от 0 до 60 прибыльных сделок из 100 сделок, то получится примерно 0.0340. Таким образом, из 100 трейдеров в минусах останется примерно 3 трейдера, а остальные 97 трейдеров увеличат свой стартовый капитал.

3.3. Выводы

По условиям задачи нам надо, чтобы было более 60% прибыльных сделок. Гипотетический сигнальщик дает верные прогнозы с вероятностью 70%. Казалось бы этого вполне достаточно, чтобы с любым количеством сделок всегда под конец быть в плюсе.

А оказывается, что это не так. Вероятностный характер прогнозов приводит к тому, что для маленького количества сделок будет очень высокая вероятность остаться в минусе. Чтобы остаться в плюсе надо провести достаточно большое количество сделок. Только тогда статистические закономерности сработают в пользу трейдера.

Но для большого количества сделок надо иметь и достаточно большой стартовый капитал. Запас стартового капитала необходим для того, чтобы в серии непрерывных убыточных сделок не произошло разорение трейдера. Отсутствие разорения нужно, чтобы трейдер после просадки своего капитала, имел на торговом счету средства, чтобы снова подняться.

Или, как вариант, если стартового капитала недостаточно и просадки приводят к разорению, то трейдер должен иметь запас финансов для нового пополнения своего торгового счета. Но это тоже требует достаточных финансов. Просто трейдер не все свои финансы сразу заводит на свой торговый счет.

Отсутствие понимания у трейдера вероятностного характера прогнозов приводит к тому, что трейдер приходит торговать с капиталом, которого хватает только на 5 или 10 сделок. В результате, с достаточно большой вероятностью такой трейдер может попасть в те самые высокие проценты тех, кто на таком количестве сделок остается в минусе. Хотя трейдер при этом применял достаточно хорошие прогнозы с высокой заходимостью и использовал очень прибыльную торговую систему.

Последнее предложение предыдущего абзаца прочитайте еще раз. Вы это поняли?