У многих трейдеров есть такое распространенное заблуждение, что, будто бы, можно достаточно хорошо прогнозировать любой рынок. Будто бы, главное, это найти для этого рынка подходящий метод прогнозирования.
Это заблуждение базируется на отсутствии у большинства трейдеров хорошего математического образования. Они думают, что раз какие-то законы управляют рынком, как об этом пишут в учебниках по трейдингу, то значит, все цены на рынке, якобы, всегда можно принципиально прогнозировать. Некоторые трейдеры даже думают, что, наверняка, существует какая-то аналитическая формула для вычисления будущих цен по предыдущим ценам. Это какая-то очень сложная крутая формула, которая до сих пор неизвестна науке.
На самом деле, всё не так просто. Прогнозируемость того или иного рынка определяется долготой "памяти" этого рынка в прошлое. То есть на сколько сильно прошлые цены влияют на будущие цены. А точнее, степень прогнозируемости рынка определяется глубиной этого влияния в прошлое.
При этом не существует резкой границы глубины этого влияния прошлого. Например, нельзя сказать, что для такого-то биржевого актива на таком-то тайм-фрейме на текущую цену влияют только цены 10 предыдущих фреймов, а цены фрейма, который был перед этими 10 фреймами никак не влияет. Нет резкой границы между ценами, которые влияют на текущую цену и ценами, которые не влияют на текущую цену. Влияние прошлого постепенно ослабевает с той или другой скоростью.
Поэтому нельзя придумать какую-то метрику данных, которая говорила бы трейдеру, что вот для этого биржевого актива на таком-то таймфрейме влияние в прошлое идет на столько-то фреймов, а на таком-то рыночном активе для такого-то тайм-фрейма влияние в прошлое идет на такое-то конкретное количество фреймов. Если бы такая метрика была возможна, то трейдер видел бы, что один рынок более случайный (короткая глубина влияния в прошлое), а другой рынок более предсказуемый (длинная глубина влияния в прошлое).
Но, всё каки есть некоторые метрики данных, которые позволяют трейдерам судить о том, на сколько случайный тот рынок, на котором они собирваются торговать, на сколько этот рынок принципиально можно прогнозировать. Самая важная такая метрика данных, это Коэффициент Неслучайности.
1. Что такое Коэффициент Неслучайности
Коэффициент Неслучайности, это формальный показатель того, на сколько данные близки или далеки от чисто случайных данных. При этом, чисто случайными данными считаются данные без "памяти", то есть такие данные, у которых цена закрытия текущего фрейма никак не зависит от цены закрытия предыдущего фрейма и цен закрытия нескольких более ранних фреймов. А степень отличия от таких чисто случайных данных определяется по степени отличая распределения непрерывных серий возрастания или убывания цены от распределения для чисто случайного процесса.
Итак, чисто случайный процесс имеет какое-то распределение непрерывных серий возрастания цены и убывания цены. Мы смотрим, а какое распределение непрерывных серий возрастания и убывания цены имеют наши данные. Если это распределение на наших данных точно совпадает с распределением на чисто случайных данных, то наши данные тоже чисто случайные. Значит, прогнозировать такие данные не имеет никакого смысла. И, соответственно, торговать на таком рынке тоже нельзя!
А если совпадения нет, то смотрим, на сколько эти распределения отличаются друг от друга. Чем сильнее отличие, тем больше наши данные отличаются от чисто случайных. То есть, тем больше наши данные неслучайные. А значит, тем наши данные будут лучше прогнозироваться методом прогнозирования, который адекватен нашим данным.
Таким образом, если ваш рынок достаточно случайный, то заработать на нем, принципиально, не получится ни с какими стратегиями заработка. А вот если ваш рынок достаточно неслучайный, то тут всё зависит от метода прогнозирования, который вы применяете на нем. С хорошей стратегией прогнозирования вы можете заработать на неслучайном рынке. А с плохой стратегией заработка вы не сможете заработать даже на неслучайном рынке.
Итак, неслучайность рынка, это необходимое условие заработка, но еще недостаточное условие для заработка.
2. Особенности Коэффициента Неслучайности
Важно хорошо понимать следующие особенности Коэффициента Неслучайности (КН):
- КН говорит нам только о том, на сколько рынок является прогнозируемым по направлению изменения цены. Коэффициент Неслучайности ничего не говорит нам о том, на сколько точно можно прогнозировать конкретное значение цены закрытия будущего фрейма. Понятно, что если нельзя прогнозировать даже направление изменения цены, то не имеет никакого смысла ставить вопрос о конкретном числовом значении прогноза.
- При вычислении КН используют только такие фреймы, в которых было изменение цены, то есть цена закрытия фрейма отличается от цены открытия фрейма. Те фреймы, на которых не произошло изменение цены (цена закрытия равна цене открытия фрейма), не участвуют в подсчете КН. Поэтому на сильно мартингальном рынке может оказаться недостаточно данных для вычисления Коэффициента Неслучайности.
3. Характерные значения Коэффициента Неслучайности
Коэффициент Неслучайности (КН) может находиться в пределах от 0 до 1 (0 ≤ КН ≤ 1). Посмотрим, на его характерные значения:
- КН = 0. Такой Коэффициент Неслучайности имеет место для чисто свингерного рынка, когда цена меняет своё направление на каждом фрейме. Глубина "памяти" в прошлое равна всей длине данных. Такой рынок абсолютно прогнозируемый по направлению изменения цены.
- 0 < КН < 1/3. Это промежуточные данные между чисто случайным рынком и чисто свингарным рынком. Чем меньше КН, тем рынок ближе к чисто свингерному рынку, и тем лучше он прогнозируется по направлению изменения цены. Чем КН ближе к 1/3, тем у рынка короче "память".
- КН = 1/3. Коэффициент Неслучайности для чисто случайных данных. В этих данных цена не зависит от предыдущих данных. Глубина "памяти" в прошлое равна нулю. Это абсолютно непрогнозируемый рынок.
- 1/3 ≤ КН ≤ 1. Это промежуточные данные между чисто случайным рынком и чисто трендовым рынком. Чем больше КН, тем рынок ближе к чисто трендовому рынку, и тем лучше он прогнозируется по направлению изменения цены. Чем КН ближе к 1/3, тем у рынка короче "память".
- КН = 1. Такой Коэффициент Неслучайности имеет место для чисто трендового рынка, когда цена на каждом фрейме только растет и нет фреймов с падением цены, или, наоборот, цена на каждом фрейме только падает и нет фреймов с ростом цены. Глубина "памяти" в прошлое равна всей длине данных. Такой рынок абсолютно прогнозируемый по направлению изменения цены.
Это, в принципе, все основные сведения о Коэффициенте Неслучайности, которые должен знать любой трейдер. Если вам этого мало, и вы хотите понимать КН на более продвинутом уровне, то читайте дальше.
4. Распределения непрерывных серий роста и падения цены
Немного отвлечемся от трейдинга и посмотрим, что такое распределение непрерывных серий.
4.1. Распределения непрерывных серий для случайных процессов
Сначала посмотрим, как распределены непрерывные серии для чисто случайных процессов.
4.1.1. Распределения непрерывных серий для подкидывания монеты
Подбрасывание монеты, это пример случайного процесса, так как выпадение орла или решки не зависит от того, орел или решка выпали на предыдущем броске монеты. У процесса подбрасывания монеты нулевая "память".
4.1.1.1. Конечное число бросаний монеты
Мы 50 раз подкинули монету и записали результат в виде 1, если выпал орел, и 0, если выпала решка. Вот, что получилось.
11011010010111110100001100110001001100111001110001
Так как вероятность выпадения орла равна 1/2 и вероятность выпадения решки тоже 1/2, то нулей и единиц должно быть примерно равное количество. Не обязательно точно равное друг другу. Здесь 26 единиц и 24 нулей.
А теперь посчитаем, сколько у нас непрерывных серий разной длины единиц и нулей. Непрерывная серия, это когда подряд идут только одни единицы или идут только одни нули. Понятно, что если, например, идут подряд 3 единицы, то это одна серия единиц длины 3, две серии единиц длины 2 и три серии единиц длины 1. Данные по подсчету представлены в таблице ниже.
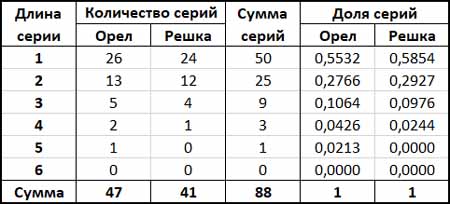
Всего было 88 серий. Это 47 серий с единицами и41 серия с нулями. Если разделить количество каких-то серий единиц на 47, то получим долю выпадения таких серий единиц среди всех серий единиц. Например, орлы по два раза подряд выпадали 13 раз. Если 13 разделить на 47, то получаем долю 0.2766. Аналогично и для серий нулей.
В последних столбцах показаны эти доли выпадения орлов и решек. Суммы этих долей, естественно, равны 1.
Также обратим внимание, что серий длины 1 ровно столько, сколько раз выпадали орлы и решки. И сумма этих серий равно 50 броскам монеты.
4.1.1.2. Бесконечное число бросаний монеты
А что будет, если количество бросков монеты устремить в бесконечность?
В этом случае количество всех серий тоже устремится в бесконечность. Но доли выпадения серий устремятся к конечным пределам. Эти пределы называются вероятностями выпадения серий определенной длины.
Вот как выглядит распределение этих вероятностей по длинам серий.
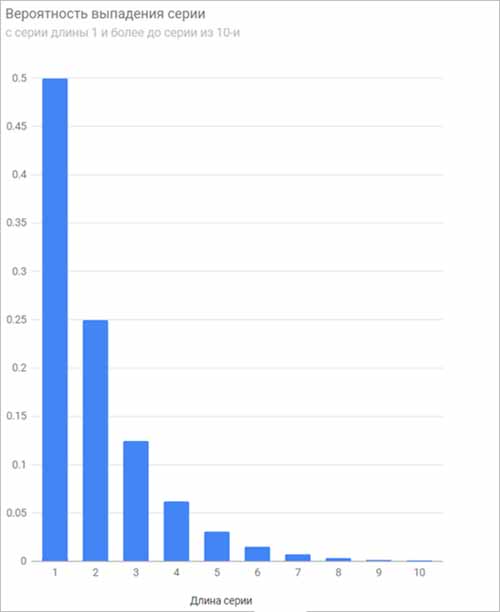
Такое будет распределение и для выпадений серий орлов и для выпадений серий решек, так как, чем больше число бросаний, тем больше симметрии между орлами и решками. Вероятность выпадения серии длины 1 здесь уже точно равна 1/2, так как в половине всех случаев выпадает орел, а в половине всех остальных случаев выпадает решка.
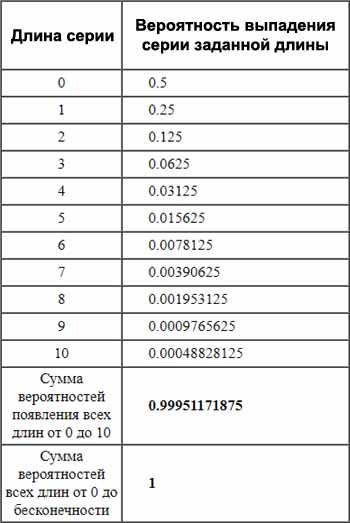
В таблице ниже показаны все вероятности выпадения серий до серии длины 10.
4.1.2. Распределения непрерывных серий для рулетки
Рассмотрим слегка асимметричный случай. Посмотрим распределения вероятностей для примера, когда в рулетке делают ставки на красное и черное. Рулетка, это тоже очень хороший пример данных с нулевой "памятью".
Асимметрия рулетки связана с тем, что там есть сектор zero. И это zero выпадает гораздо чаще, чем подброшенная монета становится на ребро.
Мы будем рассматривать непрерывные серии выпадения красного и непрерывные серии выпадения некрасного. Серия выпадения некрасного, это такая непрерывная серия в которой может встречаться только черное или zero в любых комбинациях.
Строить гистограммы распределений и их таблицы будем в этом удобном Продвинутом Калькуляторе Мартингейла.
Пусть для определенности у нас будет европейский вариант рулетки. В европейской рулетке 37 секторов, 18 красных и 18 черных. Значит, вероятность выпадения красного уже не 0.5, а 18/37 = 0.4864865. А вероятность выпадения некрасного 19/37 = 0.5135145. Сумма этих вероятностей равна 1.
Подставляем эти вероятности в Калькулятор Мартингейла в поле ввода "Какой процент всех сделок является прибыльным" (в процентах: 48.64865 и 51.35145). Другие данные подставляются на ваше усмотрение, так как на распределения вероятностей влияет только вероятность выпадения нужного исхода.
В результате получаем два таких распределения.
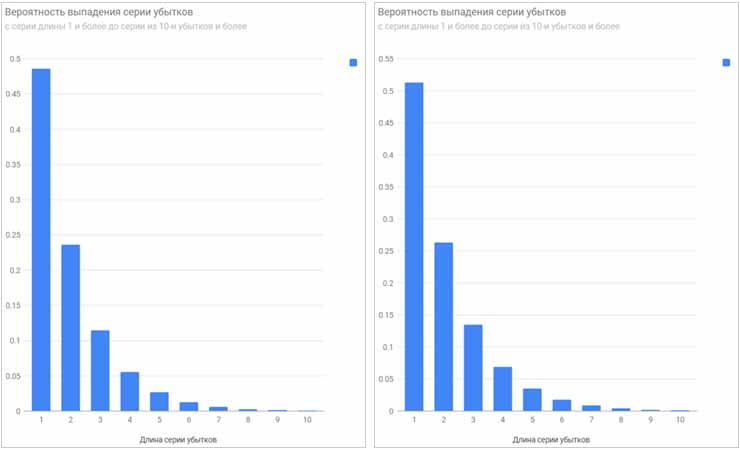
Слева вероятности выпадения серий красного, а справа вероятности выпадения серий некрасного. (Не обращайте внимание на фразы про серии убытков на гистограммах. Это специфическая особенность Калькулятора Мартингейла, он по обратной вероятности строит распределения, которые считает убыточными для игрока.)
Гистограммы слегка отличаются друг от друга. Поэтому приведем здесь дополнительно таблицы вероятностей появления серий разной длины.
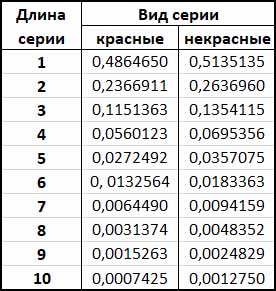
Если рулетка честная, то имено так распределяются непрерывные серии выпадения красного и некрасного для чисто случайного процесса с вероятностью красного 18/37 и вероятностью некрасного 19/37.
4.1.3. Распределения непрерывных серий для кубика
Теперь посмотрим на распределения серий, когда снова имеем только два исхода, но вероятности этих исходов очень сильно отличаются.
Бросание кубика, это еще один пример чисто случайного процесса с нулевой "памятью".
Будем считать одним исходом бросания кубика выпадение шестерки. А вторым исходом выпадение любого числа кроме шести. Соответственно, будем рассматривать непрерывные серии последовательного выпадения только шестерок, и непрерывные серии, которые содержать любые числа в любом порядке, кроме шестерок.
Вероятность выпадения шестерки равна 1/6 = 0.1666667. Вероятность выпадения любого числа, кроме 6, будет 5/6 = 0.8333333. Подставляем в Продвинутый Калькулятор Мартингейла вероятности в процентах: 83.33333 и 16.66667. В результате получаем следующие распределения выпадения непрерывных серий.
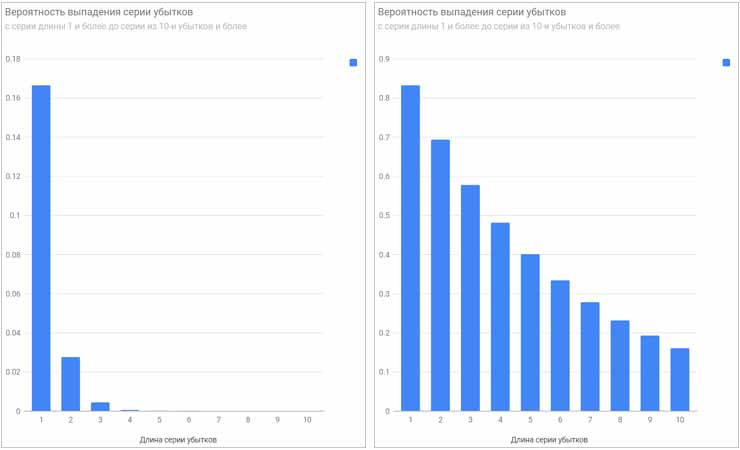
Итак, чисто случайные процессы с нулевой "памятью" имеют свои характерные распределения частот появления непрерывных серий. Вид этих распределений зависит только от вероятности наступления таких событий, серии которых мы рассматриваем.
Например, если рассматриваемое поведение рыночной цены является чисто случайным, а вероятность того, что цена пойдет вверх будет 1/6 и вероятность того, что цена пойдет вниз будет 5/6, то серии фреймов с ценой вверх и серии фреймов с ценой вниз будут распределены точно также, как в нашем примере с кубиком.
Цена пойдет вверх с вероятностью 1/6 означает, что на рассматриваемом участке примерно в 16.66667% все фреймы имеют повышение цены. Цена пойдет вниз с вероятностью 5/6 означает, что на рассматриваемом участке примерно в 83.33333% все фреймы имеют понижение цены.
Если обнаружится существенное отклонение от распределений, которые соответствуют этим вероятностям для чисто случайного процесса, то значит, эта рыночная цена не является чисто случайной. А значит, её можно прогнозировать.

