Метрика R2 Коэффициент Детерминации

Большинство трейдеров считают, что коэффициент детерминации R², это самая бесполезная метрика прогнозирования рыночных цен. Такая ситуация сложилась из-за того, что трейдеры плохо понимают природу этой метрики и того, что это метрика показывает на самом деле.

Дело в том, что эта метрика, в какой-то степени, одноразовая. Её надо смотреть только один раз, когда вы переходите к новому методу прогнозирования цен или старый метод прогнозирования цен пытаетесь применять на новых данных.

Коэффициент детерминации R², на самом деле, показывает адекватность метода прогнозирования к тем данным, на которых выполняется прогнозирование этим методом. Поэтому и смотрим на R² только один раз на самом первом прогнозе, чтобы убедиться в адекватности, а далее уже сравниваем разные прогнозы, например, по метрике RMSE.

1. Что такое R²

Коэффициент Детерминации R² вычисляется по краткой формуле:

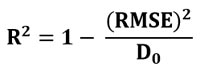
Здесь D₀, это дисперсия реальных значений цены на тестовых фреймах:

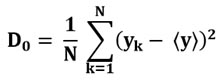
Здесь N, это количество тестируемых точек (фреймов) на тестовых данных, y_k, это реальное значение k-ой по счету цены закрытия, а <y>, это среднее значение цен закрытия на тестовых фреймах.

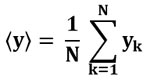
А RMSE, это главная метрика качества прогнозирования цен. Напоминаю её формулу (все обозначения см. в статье про RMSE на этом сайте):

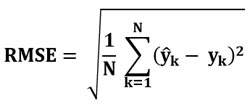
Поэтому краткую формулу для Коэффициента Детерминации можно переписать в виде подробной формулы:

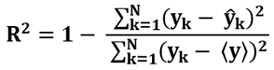
Итак, всё очень просто. Чтобы получить коэффициент детерминации R² надо от единицы отнять отношение среднеквадратичной ошибки прогнозов к среднеквадратичному отклонению прогнозов от среднего значения цены.

2. Где и когда вычисляется Коэффициент Детерминации

Напоминаю, что ваши исторические данные котировок разбиваются на две части:

• Первые 80% всех введенных вами данных используются для обучения нейросети
• Последние 20% всех введенных вами данных используются для тестирования нейросети

Когда нейросеть учится прогнозировать на обучающих данных, её на каждом шаге (эпохе обучения) проверяют на тестируемых данных. Это необходимо, чтобы заметить тот момент, когда прогнозы на тестовых фреймах перестают улучшаться. Если обнаружено, что дальнейшее обучение нейросети не улучшает прогнозы на тестовых данных, то дальнейшее обучение прекращают.

Вот в этот самый момент на тестовых данных и вычисляется Коэффициент Детерминации R².

3. Суть Коэффициента Детерминации R²

3.1. Проблема первого прогноза

Допустим, у вас есть какой-то метод прогнозирования. Неважно какой. Это может быть или нейросеть, или метод скользящих средних, или уровни Фибоначчи и т.д. И, допустим, вы для проверки своего метода прогнозирования сделали несколько каких-то прогнозов на исторических данных.

Как вам понять, адекватный ли у вас метод прогнозирования?

Как понять, можно ли этим методом прогнозирования, в принципе, прогнозировать эти данные?

Если бы у вас были бы два разных метода прогнозирования, которыми вы сделали бы два прогноза на одних и тех же исторических данных, то вы просто посчитали бы у этих двух прогнозов RMSE. После чего сказали бы, что тот метод, который дает меньшее значение RMSE, является более лучшим методом прогнозирования.

Точно также, если бы у вас был бы только один метод прогнозирования, но вы сделали им два прогноза на двух разных исторических данных, то вы бы тоже посчитали бы два RMSE на этих прогнозах. После чего сказали бы, что те данные, на которых меньше RMSE, более адекватны вашему методу прогнозирования.

Но как быть, если прогноз только один?

3.2. Прогноз нулевого уровня

На самом деле, когда мы хорошо знаем наши данные, то мы глядя на RMSE можем интуитивно сообразить, что прогноз очень плохой или очень хороший. Например, если мы прогнозируем валютную пару EUR/USD и получаем, что RMSE≈1, то мы ситаем, что это плохой метод прогнозирования. Ведь мы же помним, что валютная пара EUR/USD давно уже болтается где-то между 1.0 и 1.5. А тут прогноз с отклонениями порядка 1.0.

Вот и получается, что самый первый прогноз надо всегда сравнивать со средним значением цены на тестовых исторических данных.

Среднее значение цены, это, прогноз нулевого уровня. Среднее значение цены, это самый плохой прогноз, но который еще имеет хоть какой-то смысл. Более худшие прогнозы, чем среднее значение, уже не имеют никакого смысла. В этом смысле, какие прогнозы считаются уже неадекватными. Если ваш метод прогнозирования дает прогнозы хуже, чем прогнозы средним значением, то ваш метод прогнозирования неадекватен для данного рыночного актива на данном таймфрейме в данное время.

Поэтому любой метод прогнозирования, в первую очередь, проверяется на свою адекватность для прогнозирования выбранного актива, выбравнного таймфрейма и выбранного времени. Если вы нашли какой-то метод прогнозирования, то в первую очередь надо проверить, что дает лучше прогнозы, ваш метод или среднее значение на тестовых данных.

3.3. Коэффициент Детерминации R² как индикатор адекватности

Если теперь посмотреть на подробную формулу Коэффициента Детерминации, то становится понятен его смысл. В числителе дроби стоит сумма квадратов отклонений реальных цен от их прогнозов, а в знаменателе находится сумма квадратов отклонений реальных цен от их среднего значения. То есть, фактически, R² показывает нам, к чему реальные цены ближе, к их прогнозам или к их среднему значению.

• Если R² < 0, то значит, выбранный метод прогнозирования является неадекватным на выбранных данных. Здесь RMSE > D₀. То есть, реальные цены находятся ближе к своему среднему значению, чем к своим прогнозам. Поэтому прогнозировать цены их средним значением здесь будет более правильным, чем прогнозировать выбранным методом прогнозирования. Прогноз нулевого уровня работает лучше, чем прогнозы выбранного метода прогнозирования.
• Если R² = 0, то значит, выбранный метод прогнозирования ничем не лучше и не хуже прогноза средним значением цены. Здесь RMSE = D₀. То есть, прогнозы отклоняются от своих реальных цен примерно также, как среднее значение цен отклоняется от реальных цен. Это тоже означает, что вместо выбранного метода прогнозирования можно прогнозы делать средним значением цены. Выбранный метод прогнозирования работает не хуже и не лучше, чем прогноз нулевого уровня. А так как прогноз нулевого уровня проще, то его и выбираем вместо разработанного метода прогнозирования.
• Если 0 < R² < 1, то значит, выбранный метод прогнозирования является адекватным для выбранных данных. Здесь RMSE < D₀. То есть, прогнозы лежат к реальным ценам более близко, чем реальные цены к их среднему значению. Поэтому можно сказать, что выбранный метод прогнозирования, как минимум, хоть что-то прогнозирует. Чем R² ближе к 1, тем RMSE ближе к нулю, то есть тем прогнозы ближе, в среднем, прижимаются, к реальным ценам.
• Если R² = 1, то такое никогда не бывает. Это означает, что все прогнозы на тестовых исторических данных совпали с реальными значениями цен. То есть прогнозы имеют нулевую ошибку: RMSE = 0. Но такое не может быть, так как любые прогнозы на рынке всегда носят только вероятностный характер. А нулевая ошибка прогноза имеет место только при отсутствии вероятностного характера.

Итак, Коэффициент Детерминации нам нужен только для того, чтобы увидеть, что он положительный, и тем самым убедиться в том, что мы имеем дело с адекватными прогнозами. Мы должны убедиться в том, что наш метод прогнозирования лучше, чем тривиальные прогнозы нулевого уровня.

В этом смысле, этот коэффициент и является одноразовым. Один раз взглянули и убедились, что метод прогнозирования адекватен выбранному рыночному активу, выбранному таймфрейму и выбранному времени прогнозирования.

Когда трейдер использует какой-то метод прогнозирования (не обязательно нейросети), то первое, что должен сделать трейдер, это провести тест на каких-нибудь недавних исторических данных. Сначала надо выбрать рыночный актив, таймфрейм, последние данные для которых будете вычислять цены, и затем надо по прогнозам и реальным ценам вычислить R². Затем смотрим на знак у полученного R², и делаем вывод.

Советую всем любителям интуитивной торговли проверить свой R². Попробуйте, например, не смотреть на график последних 10 фреймов и начертить от руки, как должен пойти график цен закрытия этих фреймов. Или попробуйте прямо сейчас нарисовать график цен закрытия будущих 10 фреймов, а когда эти 10 фреймов закроются, то посмотрите, какой получился R² у вашей интуиции. Вот и увидите, на сколько ваша интуиция адекватна выбранному рынку.

4. Примеры разных R²

В этом разделе рассмотрим несколько примеров для того, чтобы у читателя сформировалась правильная интуиция понимания Коэффициента Детерминации.

На первом графике показаны цены закрытия одной из криптовалют на 30 последовательных фреймах. Но тестовыми фреймами, на которых будем тестировать разные методы прогнозирования на их адекватность, у нас будут только последние 11 фреймов с 10-го по 30-ый. Поэтому среднее значение цен закрытия показано горизонтальной линией только для этих 11 фреймов. Это среднее значение цены равно примерно 506.

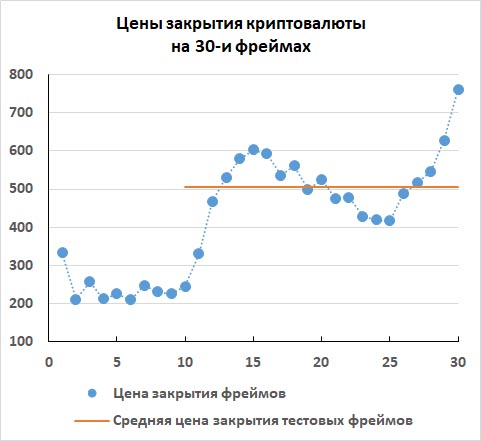
Будем считать, что это последние фреймы с известными ценами закрытия, и нам надо понять, можно ли сделать прогноз цены закрытия будущего 31-го фрейма каким-нибудь из методов прогнозирования. По Коэффициенту Детерминации мы хотим узнать, будут ли наши методы прогнозирования адекватными для этой криптовалюты или нет.

4.1. Прогноз номер 1

Первый прогноз очень хорошо коррелирует с реальными ценами. Он не только правильно определил направления трех глобальных трендов реальных цен, но и отследил даже мелкие колебания цены на втором нисходящем тренде.

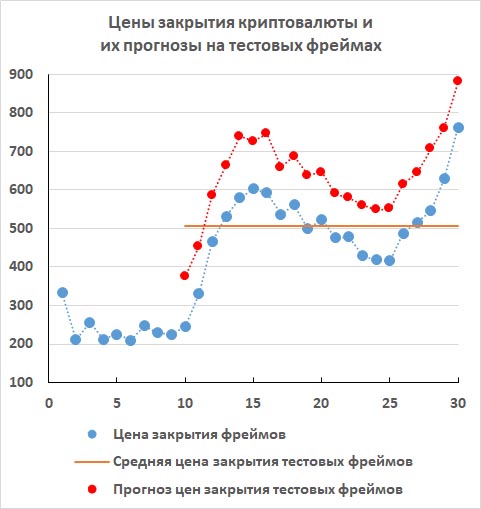
И тем не менее, это жутко неадекватный прогноз. На графике сразу видно, что прогнозы лежат слишком высоко от реальных цен. Поэтому расстояния от реальных цен до горизонтальной линии средних цен гораздо меньше, чем расстояния между реальными ценами и их соответствующими прогнозами. Для данного прогноза на данных тестовых фреймах получается R² ≈ - 1.54. Метод прогнозирования неадекватен. Этим методом прогнозировать цену закрытия 31-го фрейма нельзя.

4.2. Прогноз номер 2

Второй метод прогнозирования лежит не выше и не ниже реальных цен. Среднее значение прогнозных цен примерно равно тоже 506.

Но и этот метод прогнозирования тоже неадекватный. Цены в прогнозе очень сильно разбросаны около их среднего значения. Поэтому снова расстояния от реальных цен до горизонтальной линии средних цен гораздо меньше, чем расстояния между реальными ценами и их соответствующими прогнозами.

Для второго метода прогнозирования получается R² ≈ - 3.68. То есть его неадекватность еще более сильная, чем у первого метода прогнозирования. Разумеется, что нет даже и речи, чтобы вторым методом прогнозировать будущий 31-й фрейм.

4.3. Прогноз номер 3

У третьего метода прогнозирования прогнозы тоже оказались не выше и не ниже реальных цен. И среднее значение цен в прогнозе тоже оказалось примерно равным 506. Отличие от второго метода прогнозирования только в том, что нет такого большого разброса цен в прогнозе. Все прогнозы лежат около своего среднего значения.

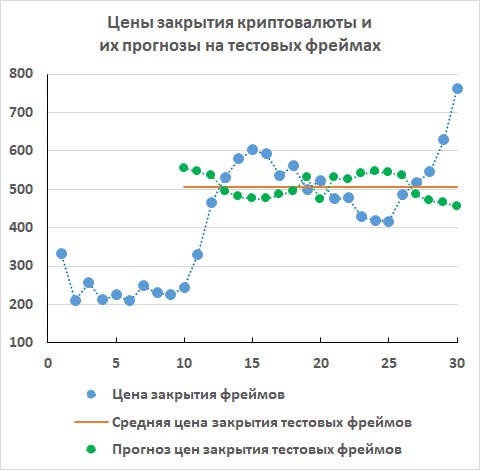
И третий метод прогнозирования тоже оказался неадекватным. Если бы все прогнозы легли бы на прямую средних значений, тогда было бы в точности R² = 0. А если бы маленькие отклонения от средних коррелировали бы с реальными ценами, как для первого прогноза, то было бы даже R² > 0. Но в нашем случае прогнозы, наоборот, антикоррелируют с реальными ценами.

Для третьего метода прогнозирования получилось R² ≈ - 1.95. Это даже хуже, чем для первого метода. Прогнозировать третьим методом на 31-м фрейме нельзя.

4.4. Прогноз номер 4

Четвертый метод прогнозирования очень хорошо обнаружил большие скачки цен в начале и в конце тестового периода. Но в середине тестового периода метод прогнозирования не смог обнаружить менее ярко выраженный пологий нисходящий тренд. Вместо этого тренда прогнозируется боковой тренд или слегка выраженный восходящий тренд.

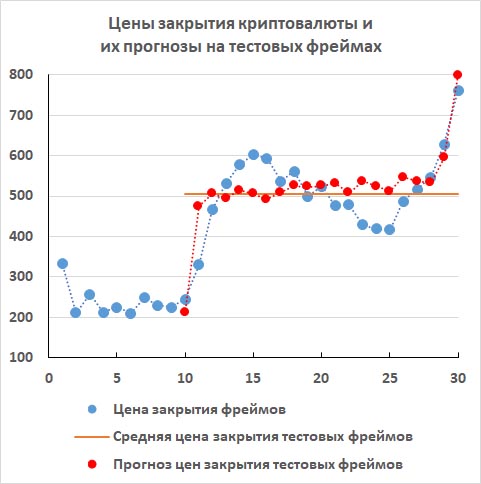
Тем не менее, достаточно хорошие прогнозы двух сильных коротких трендов перевесили плохой прогноз более пологого тренда и, в целом, на тестовом периоде четвертый метод прогнозирования оказался адекватным. Четвертый метод прогнозирования уловил глобальную тенденцию роста цены на всем тестовом периоде. Трейдер с таким методом прогнозирования оказался бы в небольшом плюсе, если бы торговал на этом тестовом периоде.

Коэффициент Детерминации для четвертого метода прогнозирования R² ≈ + 0.25. Он больше нуля. Значит, этим методом можно попытаться прогнозировать цену закрытия будущего 31-го фрейма.

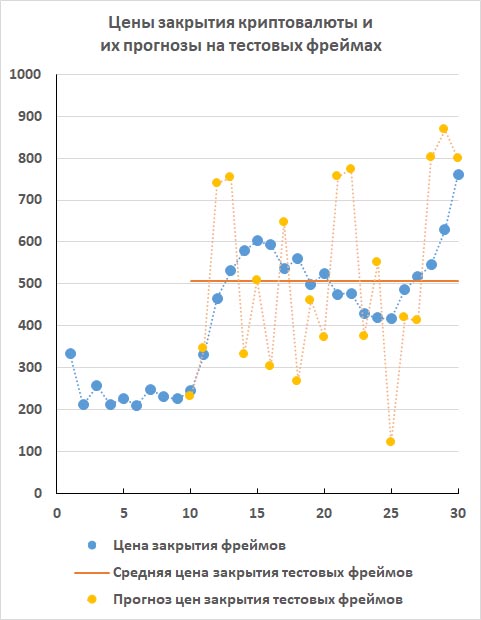
4.5. Прогноз номер 5

Наконец, пятый метод прогнозирования обнаружил не только сильные короткие восходящие тренды в начале и в конце тестового периода, но и откат между этими трендами. Причем, в этом среднем нисходящем тренде метод прогнозирования сумел обнаружить даже и некоторые слабые откаты вверх.

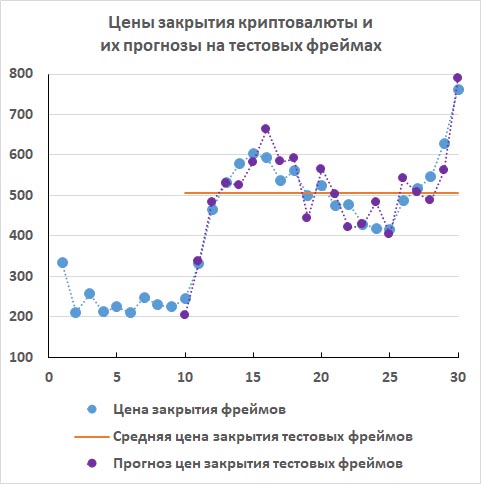
Даже простым взглядом видно, что реальные цены находятся гораздо ближе к их прогнозам, чем к горизонтальной линии их средних значений. Коэффициент Детерминации для пятого метода прогнозирования R² ≈ + 0.70 и положителен и больше, чем R² для четвертого метода прогнозирования.

Это значит, что пятым методом не только тоже можно прогнозировать цену закрытия будущего 31-го фрейма, но пятый метод, как раз, более желателен для такого прогноза. Оба последних метода прогнозирования адекватные. Но так как дисперсия реальных цен закрытия D₀ на тестовом интервале одинаковая для этих методов, то получается, что RMSE для пятого метода меньше, чем для четвертого метода.

Для приведенных здесь реальных цен закрытия тестовых фреймов D₀ ≈ 11681. Применяя краткую формулу для R², получаем:

• RMSE ≈ 93.60 для четвертого метода прогнозирования
• RMSE ≈ 59.20 для птого метода прогнозирования

5. Где искать R² в результатах прогноза

В результатах прогноза нейросети "Прогнозирующая Машина" вы можете посмотреть Коэффициент Детерминации в главной таблице результатов прогноза. Здесь показан пример таблицы результатов и зеленой линией обведенена та колонка, в которой смотрим получившийся R².

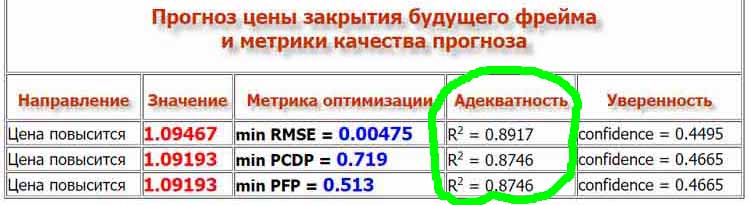
Нейронная сеть "Прогнозирующая Машина" обучается 3 раза. В каждом её обучении делается оптимизация по одной из метрик прогнозирования:

• RMSE
• PCDP
• PFP

Поэтому, в общем случае, онлайновый калькулятор этой нейросети выдает 3 разных прогноза будущей цены биржевого актива. Каждая строка таблицы соответствует прогнозу с оптимизацией обучения по одной из этих 3-х метрик. Затем на тестовых исторических данных вычисляется R². Так как это 3 разных обучения, то, соответственно, в общем случаем, у нас все 3 значения R² могут не совпадать друг с другом.

Обучение нейросети на обучающих исторических данных заканчивается, когда метрика, по которой идет оптимизация, принимает своё наилучшее значение на тестовых исторических данных. Например, если оптимизируем обучение нейросети по метрике RMSE, то обучение заканчивается, когда RMSE перестает уменьшаться на тестовых данных. Вот, когда метрика RMSE минимальная, тогда и вычисляем R², который соответствует минимуму RMSE.

Аналогично, вычисляем Коэффициенты Детерминации, когда на тестовых фреймах получаются максимальные значения метрик PCDP и PFP.

Поэтому и получаются 3 варианта R².

Вы можете заметить, что все три типа оптимизации иногда дают одинаковые значения Коэфициента Детерминации, а иногда все три значения разные. Еще бывают случаи, когда два из трех Коэффициентов Детерминации равны между собой, но не равны третьему R².

Почему так?

Если вы посмотрите еще раз на краткую формулу Коэффициента Детерминации, то увидите, что дисперсия D₀ цен закрытия на тестовых данных всегда одна и та же, так как тестовые данные не меняются в зависимости от выбранной оптимизации. А вот RMSE не обязан быть всегда таким же минимальным, каким эта метрика бывает при оптимизации по ней.

При других видах оптимизации, в общем случае, метрика RMSE может или быть равной своему минимальному значению или может быть больше своего минимального значения. В первом случае R² будет точно таким же, как и при оптимизации по RMSE. Во втором случае R² будет меньше, чем Коэффициент Детерминации при оптимизации по RMSE.

В приведенной выше таблице как раз и показан такой случай, когда оптимизация по PCDP и по PFP не дает минимального значения RMSE. И, как следствие этого, значения R² для этих оптимизаций меньше, чем при оптимизации по RMSE.