Часто, трейдеры хотят, чтобы в качестве метрики качества прогнозирования была прибыль трейдера. То есть они хотят оценивать метод прогнозирования по такому критерию, как заработок трейдера.
Но на самом деле, это очень плохой подход. Такой подход говорит о непрофессионализме трейдера, о том, что трейдер не понимает, что по критерию прибыли можно оценивать только торговые системы. А прогнозы не являются торговой системой, так как в прогнозах никак не учитывается финансовый менеджмент.
Такие вещи, как доля капитала на сделку, минимальный депозит, минимальный капитал на сделку, корреляции между результатами сдедок и т.п. никак не вносятся в начальные данные для получения прогноза и никак не вычисляются в результате прогноза. Поэтому трейдеры должны оценивать качество прогнозов рыночных цен по метрикам, которые приняты в математике.
Рассмотрение метрик прогнозирования начнем с самой важной метрики RMSE.
1. Что такое RMSE
RMSE (Root Mean Squared Error), это корень квадратный из среднеквадратичной ошибки прогноза.
Эта метрика показывает, на сколько, в среднем, прогноз отклоняется от реальных значений рыночной цены. Вычисляется RMSE по формуле:
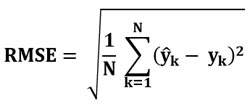
Здесь N, это количество тестируемых точек (фреймов), yk, это реальное значение k-ой по счету цены, которое надо прогнозировать на тесте, а yk со шляпкой, это значение k-ой по счету цены, которое выдал прогноз.
Итак, всё очень просто. Мы сначала берем разницу цен между прогнозом и реальной ценой, возводим все эти разницы цен в квадрат и усредняем по всем N тестовым случаям. И, наконец, из полученного среднеквадратичного отклонения извлекаем квадратный корень.
2. Где вычисляется RMSE
Введенные вами исторические данные котировок рыночных активов разбиваются на две части:
- Первые 80% всех введенных вами фреймов считаются обучающими фреймами
- Последние 20% всех введенных вами фреймов считаются тестовыми фреймами
На обучающих фреймах нейросеть обучается прогнозировать. А на тестовых фреймах проверяют, как нейросеть научилась делать прогнозы. Метрика RMSE вычисляется на тестовых данных. Именно эту метрику вы видите в результатах прогнозирования нейросети Прогнозирующая Машина.
Нейросеть Прогнозирующая Машина может обучаться так, чтобы на тестовых фреймах показать самое низкое значение RMSE, которое возможно получить на введенных вами данных. При такой оптимизации обучения нейросети по минимуму RMSE нейросеть Прогнозирующая Машина прогнозирует цену закрытия будущего фрейма, которую вы видите в результатах прогнозирования вместе с минимальным RMSE, который соответствует этому прогнозу.
Чем меньше значение RMSE, тем лучше. Чем меньше значение RMSE, тем значит, более точно Прогнозирующая Машина прогнозирует цены. Минимальное значение RMSE равно нулю. Если RMSE равен нулю, то это означает, что на всех тестовых фреймах прогнозы точно совпали с реальными значениями цены.
3. Пример вычисления RMSE
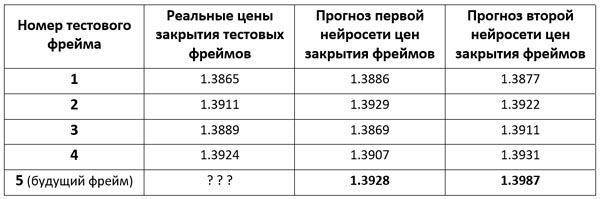
Пусть, для примера, тестовый набор состоит всего из 4-х фреймов. Рассмотрим тестовые прогнозы двух обученных нейросетей, которые показаны в двух последних колонках таблицы.
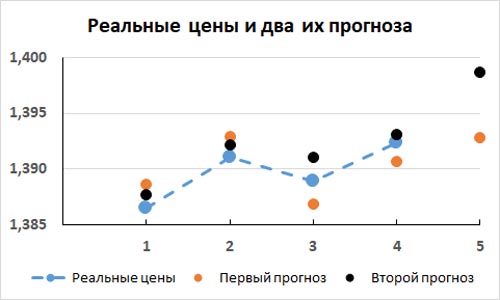
Эти два прогноза и реальные цены тестовых фреймов для наглядности показаны на этом графике.
Посчитаем RMSE сначала для тестовых прогнозов первой нейросети.
Сначала суммируем разности квадратов между прогнозами первой нейросети и реальными значениями:
(1.3886 - 1.3865)2 + (1.3929 - 1.3911)2 + (1.3869 - 1.3889)2 + (1.3907 - 1.3924)2 = 0.000014540.
Теперь для усреднения по всем тестовым фреймам делим эту сумму на число тестовых фреймов N=4, и получаем: 0.000014540 / 4 = 0.000003635.
Наконец, извлекаем из полученного числа квадратный корень, и получаем примерно: 0.0019.
Теперь вы умеете вычислять RMSE, если известны и прогнозы и реальные цены на тестовых фреймах.
Аналогично вычисляем RMSE и для второй нейросети. Получаем примерно: 0.0014.
Получается, что RMSE для прогнозов первой нейросети больше, чем для второй, причем больше на существенные 35% . Значит, вторая нейросеть прогнозирует лучше, чем первая нейросеть. Исходя из этого, мы больше доверяем прогнозам второй нейросети, а не первой.
Как видно, из таблицы и из графика, обе нейросети спрогнозировали будущий 5-й фрейм, цена закрытия которого еще неизвестна. И оба эти прогноза разные:
- Первая нейросеть прогнозирует цену закрытия будущего фрейма: 1.3928
- Вторая нейросеть прогнозирует цену закрытия будущего фрейма: 1.3987
Мы больше доверяем прогнозу второй нейросети с ценой 1.3987, так как у неё RMSE на предыдущих фреймах был меньше, чем у первой нейросети. Выбрав из двух прогнозов прогноз второй нейросети, мы меньше ошибемся, чем если выберем прогноз первой нейросети.
4. Разница между RMSE и MSE
При прогнозировании с помощью нейросетей и других методов машинного обучения иногда используют метрику MSE (Mean Squared Error). Отличие метрики RMSE от метрики MSE заключается в том, что MSE, это среднеквадратичная ошибка, а RMSE, это корень квадратный из среднеквадратичной ошибки.
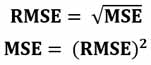
Таким образом, формула для MSE отличается от формулы для RMSE только отсутствием квадратного корня:
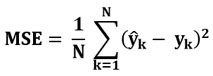
Чем прогноз лучше, тем MSE тоже меньше, как и RMSE. Но RMSE гораздо удобнее, чем MSE, потому что RMSE измеряется в тех же самых единицах, что и прогнозируемая величина. Например, если прогнозируемая цена измеряется в рублях, то величина RMSE тоже будет в рублях, а величина MSE будет иметь единицу измерения рубль в квадрате.
Например, пусть прогнозируется рублевый актив с ценами в диапазоне примерно 65-75 руб., то есть цена находится где-то около 70 руб. Если получаем качество прогноза MAE = 1225 (руб.)2, то это мало что нам говорит. Но соответствующий ей RMSE = 35 руб., сразу же нам скажет, что ошибка прогнорзирования примерно равна половине от средней цены 70 руб.
5. Разница между RMSE и MAE
Еще одной очень распространенной метрикой оценки качества прогноза является MAE (Mean Absolute Error). Это метрика тоже измеряет ошибку прогноза на тестовых данных. Но это средняя абсолютная ошибка:
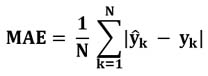
Такая формула для вычисления MAE приводит к тому, что все ошибки имеют одинаковый вес, независимо от размера ошибки. Очень большая ошибка будет учитываться с таким же весом, как и очень маленькая ошибка. Это приводит к тому, что отдельные очень большие ошибки будут оказывать слабое влияние на величину MAE, если суммируется достаточно большое количество ошибок.
Если сравнить формулы для MAE и RMSE (или MSE), то видно, что в формулах для RMSE (и MSE) величины отдельных ошибок складываются не с одинаковыми весами, а с весами равными величине самой ошибки. То есть, чем больше величина ошибки, тем с большим весом она стоит в суммировании. Это означает, что большие ошибки вносят больший вклад в RMSE и MSE, чем маленькие ошибки.
Рассмотрим пример. Пусть на 100 тестовых фроеймах абсолютная ошибка на каждом фрейме равна 1.0. Тогда MAE = 1.0 и RMSE = 1.0. Пусть теперь на каком-то одном из фреймов ошибка стала равной 5.0. Теперь MAE = 1.04, а RMSE = 1.11. А если ошибка на этом фрейме будет равна 10.0, тогда MAE = 1.09, а RMSE = 1.41.
Таким образом, линейно растущая ошибка прогнозирования на одном из фреймов приводит к тому, что MAE тоже линейно растет, а RMSE будет гораздо быстрее нелинейно расти. Если происходит такое улучшение качества прогнозирования, которое снижает особо крупные ошибки, то это сразу становится заметно по резкому снижению RMSE, а снижение MAE в этом случае может быть совсем незаметным.
Выбор между RMSE и MAE зависит от того, на сколько важны большие ошибки по сравнению с меньшими. Если большие ошибки критичны, то следует использовать RMSE. Если все ошибки имеют одинаковую важность, то следует использовать MAE. Поэтому в теме прогнозирования рыночных цен используется RMSE, так как одна большая ошибка может привести к плохим последствиям. А, например, при прогнозировании температуры используется MAE, так как в этой задаче все ошибки имеют одинаковую важность.
6. Где смотреть RMSE в прогнозах нейросети
В результатах прогноза нейросети "Прогнозирующая Машина" трейдер можете посмотреть RMSE в главной таблице результатов прогноза. Здесь показан пример таблицы результатов и зеленой линией обведенено то место, где надо посмотреть RMSE.
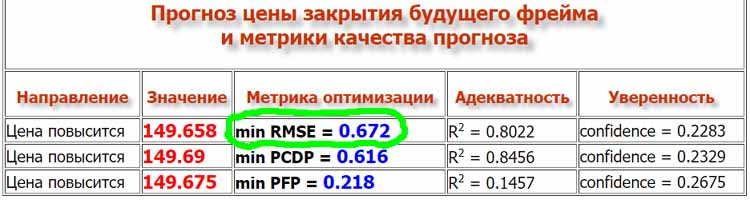
Нейросеть "Прогнозирующая Машина" обучается 3 раза. Каждый раз она обучается так, чтобы на тестовых данных была оптимальной одна из трех метрик:
Поэтому в колонке прогнозов мы видим, в общем случае, 3 разных числа, так как по разному обученные 3 нейросети прогнозируют немного разные числа.
Первый прогноз сделан как раз такой обученной нейросетью, которая обучалась так, чтобы на тестовых данных значение RMSE получилось самым минимальным. Второй и третий прогнозы сделаны так обученными нейросетями, что у них RMSE не самое минимальное на тестовом множестве. Там оптимальные значения получились у других метрик прогнозирования.
Возможно, внимательного читателя удивит тот факт, что максимальый R2 в приведенном примере оказался не в первой строке таблицы, а во второй строке (0.8022 < 0.8456). Это связано с одной из главных "фишек" калькулятора "Прогнозирующая Машина" версии 2.0. Тестовые данные для всех трех оптимизаций имеют разную длину. И на них, соответственно, разные дисперсии (см. формулу коэффициента детерминации).
Перед тем, как обучать нейросеть, сначала калькулятор делает статистический анализ введенных данных и определяет, какую глубину данных в прошлое надо взять для получения лучшего прогноза. То есть, на сколько длинная "память" у введенных данных. Понятно, что для прогноза с минимальным отклонением от верных значений цены и с минимальными ошибками направления движения цены, в общем случае, может потребоваться разные глубины данных в прошлое.

