Случайный рынок без "пямяти" в прошлое принципиально невозможно прогнозировать никакими методами прогнозирования. Это математический закон, обойти который невозможно. Иначе давно бы уже прогнозировали рулетку в казино. Наоборот, если ваши исторические данные, которые используются для получения прогноза в будущее, являются неслучайными, то они хорошо поддаются прогнозированию.
Но резкой границы между случайным и неслучайным рынками не существует. Как правило, биржевые рынки на Форексе, фондовой бирже и криптобиржах являются промежуточными между чисто случайными и чисто неслучайными. Часто временной ряд изменения рыночной цены какого-нибудь биржевого актива бывает очень близким к чисто неслучайному временному ряду. Или, наоборот, очень близким к чисто случайному временному ряду.
В первом случае заработать на таком рынке можно, так такой рынок достаточно хорошо прогнозируется. Во втором случае заработать принципиально невозможно, так как такой рынок принципиально не прогнозируется.
При использовании наших нейросетей Прима и Прогнозирующая Машина трейдер получает не только прогноз поведения цены в будущем, но и метрики используемых исторических данных. Метрики данных, это числовые показатели, которые как раз и показывают в конкретных числах, на сколько ваши данные близки к чисто случайным, или, наоборот, к чисто неслучайным.
Если ваш рынок оказался очень случайным, то любой прогноз на таком рынке надо забраковать. Не только прогноз, сделанный нашими нейросетями, но и прогноз, сделанный любым другим методом прогнозирования (любыми индикаторами, осцилляторами, паттернами, линиями, волнами, и т.д.). На таком рынке принципиально нельзя открывать позиции.
Кроме метрик данных Коэффициент Неслучайности и Коэффициент Разворотов, есть еще одна метрика, это Среднее Количество Фаз. В данной статье рассказывается про Среднее Количество Фаз.
1. Что такое Среднее Количество Фаз
Среднее Количество Фаз, это формальный показатель того, на сколько данные близки или далеки от чисто случайных данных. Степень отличия от таких чисто случайных данных определяется по сравнению среднего количества участков однородного поведения цены на рынке от числа таких участков однородного поведения цены, которое должно было бы быть на этом рынке, если бы рынок вел себя чисто случайно.
Такой участок однородного поведения цены называется Фазой. Обычно рассматривают 3 вида фаз:
- Участок с растущей ценой. Восходящий тренд.
- Участок с падающей ценой. Нисходящий тренд.
- Участок с постоянной ценой. Боковой тренд.
Так как ценовой график имеет фрактальную структуру, то, при подсчете количества фаз, учитываются только цены закрытия фреймов. Колебания цены внутри фрейма не учитывается.
При этом, чисто случайными данными считаются данные без "памяти", то есть такие данные, у которых цена закрытия текущего фрейма никак не зависит от цен закрытия одного или нескольких предыдущих фреймов.
Итак, если бы рынок был число случайным без "памяти" о своем прошлом, то на нем было бы определенное Среднее Количество Фаз. Трейдеру надо посчитать, а какое реальное Среднее Количество Фаз (СКФ) присутствует на рынке на его исторических данных, по которым он строит свой прогноз. И затем надо сравнить это число со Средним Количеством Фаз для чисто случайного рынка на такой же длинне данных.
Чем эти два числа ближе друг к другу, тем хуже. Тем выбранный рынок более случайный. А значит, заработать на нем трейдингом не получится. А вот чем эти два числа больше отличаются друг от друга, тем лучше. Тем выбранный рынок менее случайный, а значит, более прогнозируемый. И тем более вероятно, что трейдер сможет что-то заработать на таком рынке.
2. Отличие СКФ от метрики Коэффициента Разворотов
На первый взгляд может показаться, что метрика СКФ дублирует метрику Коэффициент Разворотов. Но это не так. Точнее, в общем случае, это разные метрики. Но иногда они действительно могут дублировать друг друга.
Чтобы разобраться в отличии метрики СКФ от метрики Коэффициента Разворотов давайте еще раз посмотрим на временной график цен закрытия, на котором мы учились считать Коэффициент Разворотов.
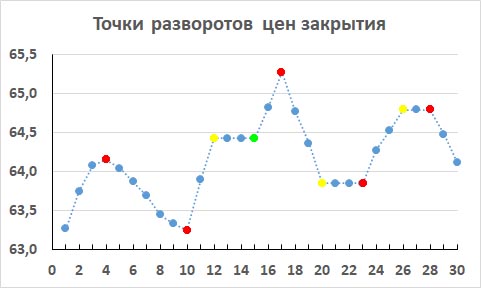
Напоминаю, что точки разворотов показаны здесь красным цветом и их тут 5 штук. Это точки с номерами 4, 10, 17, 23 и 28. Все точки разворотов всегда являются еще и точками смены фаз.
Но, кроме точек разворотов к точкам смены фаз на рисунке относятся еще и точки зеленого и желтого цветов. В этих точках меняются типы трендов, хотя ценовые развороты отсутствуют.
Итак, фазы на этом рисунке выделены синими точками, а разделители фаз выделены красными, желтыми и зелеными точками. Итого, получаем, что на рисунке у нас имеется 10 фаз, 9 точек смены фаз и 5 точек разворота.
Понятно, что точек смены фаз всегда на единицу меньше, чем количество фаз. Значит, если на ценовом графике нет участков с постоянной ценой, то число точек смены фаз будет совпадать с числом точек разворотов. И тогда метрика СКФ будет на единицу больше метрики Коэффициента Разворотов.
Итак, метрика СКФ дублирует метрику Коэффициент Разворотов только тогда, когда на ценовом графике отсутствуют участки с постоянной ценой. В этом случае СКФ всегда на единицу больше Коэффициента Разворотов.
2.1. СКФ и участки постоянной цены
Если СКФ больше Коэффициента Разворотов более чем на 1, то значит, в ваших исторических данных есть участки с постоянной ценой. Если разница на число 2, то значит, есть один такой участок, причем, на конце этого участка находится точка разворота. Как, например, участок 20-23 или 26-28 на рисунке.
Если разница на число 3, то значит, есть или два таких участка, у которых на конце точки разворотов. Как, например, участки 20-23 и 26-28 на рисунке. Или имеется только один участок с постоянной ценой без точек разворота. Как, например, участок 12-15 на рисунке.
И т.д. Например, если разница между СКФ и Коэффициентом Разворотов равна 25, то это значит, что рассматриваемый ценовой участок содержит от 12 до 24 участков с постоянной ценой. Минимум может быть (25-1)/2 = 12 участков постоянной цены без точек разворота на концах. А максимум может быть 25-1 = 24 участка постоянной цены с точками разворота на концах всех этих участков.
На нашем графике разница между СКФ и Коэффициентом Разворотов равна 10 - 5 = 5. Значит, реальное число участков постоянной цены должно быть от минимум (5-1)/2 = 2 до максимум 5-1= 4. Реально их на рисунке 3. Один участок постоянной цены без точек разворотов и 2 участка с точками разворота на концах.
3. Как СКФ сравнивается с СКФ на случайным рынке
На рынке с отсутствием "памяти" на тех же самых 30 фреймах было бы СКФ = 19.67. Реальное значение СКФ = 10 достаточно далеко отстоит от числа 19.67 для чисто случайного рынка. Поэтому на картинке изображен ценовой график не чисто случайного рынка.
Но минимальное число фаз может быть равным 1. Это имеет место, например, когда на рассматриваемых данных чисто трендовый рынок без участков с постоянной ценой. Наше реальное значение СКФ = 10 находится где-то посередине между чисто случайным значением СКФ = 19.67 и 1. То есть данный рынок прогнозируемый, но не так хорошо, как прогнозируется идеально трендовый рынок.
Когда вы делаете прогнозы рыночных цен на нашем сайте с помощью нейросети Прима и/или нейросети Прогнозирующая Машина, то в результатах вы получаете и значение реального СКФ на ваших исторических данных и то, какое было бы значение СКФ на случайном рынке на том же самом интервале ваших исторических данных. Вы можете сравнить эти данные и решить, на сколько ваш рынок является прогнозируемым.
4. Особенности СКФ
У Среднего Количества Фаз (СКФ) следующие особенности:
- СКФ (также, как и Коэффициент Неслучайности и Коэффициент Разворотов) говорит нам только о том, на сколько рынок является прогнозируемым по направлению изменения цены. СКФ ничего не говорит нам о том, на сколько точно можно прогнозировать конкретное значение цены закрытия будущего фрейма. Если нельзя прогнозировать направление изменения цены, то, естественно, не имеет никакого смысла ставить вопрос о конкретном числовом значении прогноза.
- При вычислении СКФ (в отличие от Коэффициента Неслучайности) нейтральные фреймы без изменения цены закрытия по отношению к цене открытия также не отбрасываются, как и при вычислении Коэффициента Разворотов. Но (в отличие от Коэффициента Разворотов) начало и конец участка с нейтральными фреймами всегда учитываются, как точки смены фаз и, соответственно, сам такой участок всегда подсчитывается при подсчете числа фаз.
5. Характерные значения СКФ
Обратите внимание, что СКФ не нормируется на длину интервала. Поэтому на каждом интервале СКФ для чисто случайного рынка будет иметь своё значение.
Давайте на примере в 30 фреймов посмотрим, как может выглядеть ценовой график для некоторых характерных значений СКФ:
- СКФ = 1. На всем интервале только одна фаза. Это максимально неслучайный рынок. Это либо какой-то идеальный тренд (восходящий или нисходящий) или это участок, на котором цена никогда не меняется (идеальный мартингальный рынок).
- СКФ = 19.67. Чисто случайный рынок без "памяти" в прошлое. Принципиально не может прогнозироваться никогда и ничем.
- СКФ = 29. Фазы меняются в каждой точке интервала. Это тоже максимально неслучайный рынок. Но прогнозировать его не так просто. Это может быть и чисто свингерный рынок, а может быть и смешанный рынок с чередованием скачков цены и сохранием постоянного значения цены.
Посмотрим примеры ценовых графиков для всех этих случаев.
5.1. Пример одной единственной фазы
Когда на интервале одна единственная фаза, то это может быть
- Или идеальный восходящий тренд
- Или идеальный нисходящий тренд
- Или идеальный боковой тренд
Здесь показан пример идеального восходящего тренда с одной фазой.
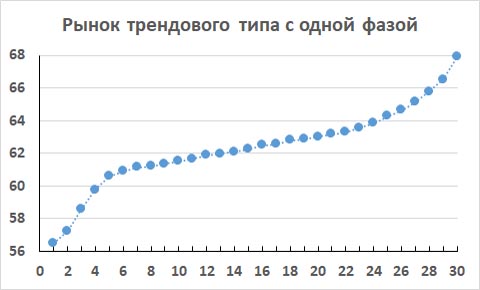
Направление цены будущего 31-го фрейма в таком тренде легко прогнозируется. Если использовать наивные методы прогнозирования, то можно сделать прогноз, что на будущем 31-м фрейме цена закрытия вырастет с вероятностью примерно p = 1.
Далее, показан пример идеального мартингального рынка с одной фазой.
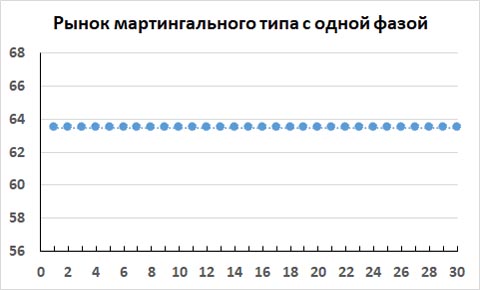
И здесь нправление цены будущего 31-го фрейма тоже легко прогнозируется. С помощью наивных методов прогнозирования делаем прогноз, что на будущем 31-м фрейме цена закрытия не изменится с вероятностью примерно p = 1.
5.2. Пример фаз случайного рынка
Это пример поведения цены на чисто случайном рынке.
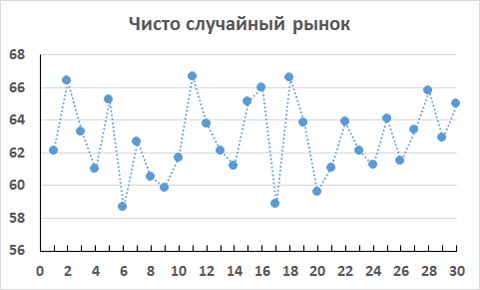
Здесь 19 фаз. Это близко к СКФ = 19.67 для чиссто случайного поведения цены на интервале 30 фреймов. Прогнозировать данный рынок невозможно никакими методами прогнозирования.
5.3. Пример максимального количества фаз
Когда количество фаз максимальное, то это может быть, например, рынок идеального свингерного типа, как на рисунке ниже.
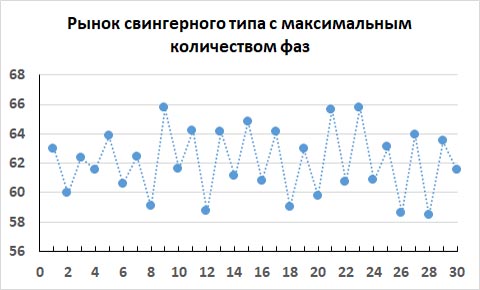
Здесь 29 фаз. Это максимально возможное количество фаз на интервале 30 фреймов. Направление цены будущего 31-го фрейма на таком свингерном рынке легко прогнозируется.
Но бывают случаи, когда сделать прогноз на рынке с максимальным количеством фаз не так просто. Следующий рисунок иллюстрирует такой случай. На нем показан график цен закрытия, который также содержит 29 фаз.
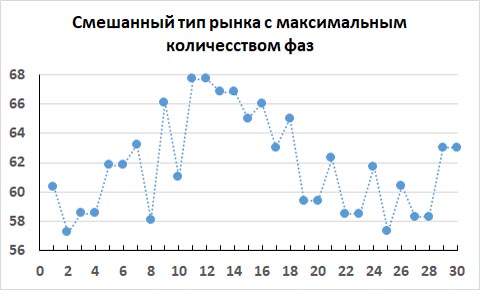
Здесь в каждой точке происходит смена фазы. Но фазы не чередуются также хорошо, как они чередовались на свингерном рынке. Поэтому направление цены для будущего 31-го фрейма не столь очевидно. Единственное, что можно сказать про 31-й фрейм, что с большой вероятностью цена не останется постоянной, а пойдет или вверх или вниз, если у рынка сохранится тенденция менять фазу на каждом фрейме.
Почему же на последнем рисунке упала способность рынка к прогнозированию? А точнее, не почему, а как это можно увидеть, что прогнозируемость стала хуже, чем на предпоследнем рисунке?
Давайте дополнительно посмотрим на метрику Коэффициент Разворотов. На предпоследнем рисунке со свингерным рынком Коэфициент Разворотов равен 28. Это максимально возможный Коэффициент Разворотов для интервала в 30 фреймов. Это говорит о том, что этот рынок хорошо прогнозируемый.
А на последнем рисунке Коэффициент Разворотов равен 17. Такой Коэффициент Разворотов не соответствует хорошо прогнозируемому рынку, так как попадает в диапазон для случайного рынка на интервале 30 фреймов.
Таким образом, при слишком большой разнице между метриками Среднее Количество Фаз и Коэффициент Разворотов, лучше прогнозируемость рынка оценивать по метрике Коэффициент Разворотов. В этом случае метрика Среднее Количество Фаз будет просто показателем того, на сколько часто на рынке встречаются мартингальные участки.

